发布于

二叉树常用方法的 JavaScript 实现

作者
  • 姓名
    Twitter

前言

好久没有更新博客了，写了好几篇没完成的文章也没办法发，就把前阵子学习的二叉树相关的代码整理一下。

本来想要写一篇关于 AVL 树的，因为我发现现在网上很难找到简洁可用的 JavaScript 代码，自己刚开始写的时候参考了几篇文章，感觉里面的代码是有错误的，比如判断左右旋上都写得非常笼统（甚至我认为是错误的），但由于近期没有进一步了解平衡二叉树，待日后完善一下再发。

这篇文章将对二叉树的一般表示方法以及常用方法进行描述，并使用 JavaScript 实现，本文为笔记性质，个人撰写代码时的注释都未删除，可供参考。

二叉树的表示

二叉链表形式

二叉树一般通过链表形式存储：

class TreeNode {
  constructor(val) {
    this.val = val;
    this.left = null;
    this.right = null;
  }
}

数组形式

对于完全二叉树可以使用数组表示，因为对完全二叉数而言，可以很容易通过数组下标确认相互关系，比如堆排序中使用的最大堆最小堆，就是直接利用数组模拟完全二叉树，进而构造最大（最小）堆，实现排序。

对于一般二叉树也可以使用数组表示，为表述清晰，会增加必要的null值，比如下图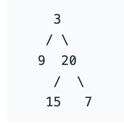： binary-tree-sample.png 用数组表示为[3,9,20,null,null,15,7]

数组表示与链表表示的互相转换

在LeetCode上做二叉树相关的题目的时候，提供的测试用例虽然是链表形式的，但由于无法直接描述，均以数组形式展示，而我们测试代码的时候需要输入的却是链表形式，很不方便。

所以需要代码进行转换，以下是本人的实现：

数组表示转化为链表表示

/**
 * @param {Array} arr
 * @return {TreeNode} 
 */
function arrayToTree(arr){
  function toNode(item){//转换数组项至节点
    if(item===null||item===undefined){return null}
    else{return new TreeNode(item)}
  }
  let queue=[];
  const tree=toNode(arr.shift());
  queue.push(tree);//入队列第一个元素
  while(arr.length>0){
  //当数组里还有项的时候就拿数组的项去填充队列
  let current=queue.shift();
  current.left=toNode(arr.shift());
  current.right=toNode(arr.shift());
  if(current.left){queue.push(current.left)}
  if(current.right){queue.push(current.right)}
  }
  return tree;
  }

链表表示转化为数组表示

之前在做判断二叉树是否为完全二叉树的时候，发现实现过程中可以顺便将二叉树转化为数组形式，与上面的方法正好相反。

/**
 * @param {TreeNode} root
 * @return {Array} 
 */
  function treeToArray(root){
    let queue=[];
    let list=[];
    queue.push(root);
    while(queue.length>0) {
      let current = queue.shift();
      if (current.left) {
        list.push(current.left.val);
        queue.push(current.left);
      }else{list.push(null)}
      if (current.right) {
        list.push(current.right.val);
        queue.push(current.right)
      }else{list.push(null)}
    }
    //我们在深度优先遍历的时候将节点保存下来，如果是null也保存，完全二叉树的性质要求我们不能有null混在值中
    //拿到这个list之后
    //第一步是将最后连续的null删掉
    let point=list.length-1;//从表最后开始看
    while(list[point]===null){
      list.pop();
      point--;
    }
    //之后再检查list中是否还有null，如果没有就是完全二叉树，有就不是
    // return list.every((item)=>{return item!==null})
    return [root.val].concat(list);//换成输出这行代码就能输出二叉树的数组表示形式，与我们前面那个arrayToBinary方法正好相反
  }

二叉树的常见题目实现

下文主要对一般二叉树实现了以下方法，其中12和14暂未完成，因为近期没有时间再看数据结构，故待日后完成后再进行补充。

下面这个列表是搜索的时候看到就复制下题目名自己进行了实现，但原始出处找不到了，不过这也不重要，毕竟并没有引用任何他人代码。

  1. 求二叉树中的节点个数
  2. 求二叉树的高度
  3. 前序遍历，中序遍历，后序遍历
  4. 分层遍历二叉树（按层次从上往下，从左往右）
  5. 将二叉查找树变为有序的双向链表（未完成）
  6. 求二叉树第K层的节点个数
  7. 求二叉树中叶子节点的个数
  8. 判断两棵二叉树是否结构相同
  9. 判断二叉树是不是平衡二叉树
  10. 求二叉树的镜像（翻转二叉树）
  11. 求二叉树中两个节点的最低公共祖先节点
  12. 求二叉树中节点的最大距离（未完成）
  13. 由前序遍历序列和中序遍历序列重建二叉树
  14. 判断二叉树是不是完全二叉树

1. 求二叉树中的节点个数

/**
 * @param {TreeNode} root
 * @return {Number} 
 */
function sizeOfTree(root){
  if(!root){return 0}
  return 1+sizeOfTree(root.left)+sizeOfTree(root.right);
}

2. 求二叉树的高度

/**
 * @param {TreeNode} root
 * @return {Number} 
 */
function heightOfTree(root){
  if(!root){return 0}
  return Math.max(heightOfTree(root.left),heightOfTree(root.right))+1
}

3. 遍历（深度优先）

遍历有递归和非递归实现，递归比较简单，非递归的话需要使用栈来模拟递归，前序遍历和中序遍历实现也较为简单，后续遍历相对复杂，此处暂时只列递归算法。非递归以及空间复杂度为O(1)的 Morris 遍历待补充。

前序遍历

function preOrderTraversal(root) {
  console.log(root.val);
  if(root.left){preOrderTraversal(root.left)}
  if(root.right){preOrderTraversal(root.right)}
}

中序遍历

function inOrderTraversal(root) {
  if(root.left){inOrderTraversal(root.left)}
    console.log(root.val);
  if(root.right){inOrderTraversal(root.right)}
}

后序遍历

function postOrderTraversal(root) {
  if(root.left){postOrderTraversal(root.left)}
  if(root.right){postOrderTraversal(root.right)}
  console.log(root.val);
}

4. 分层遍历（广度优先）

深度优先遍历使用栈，广度优先则使用队列。

function BFS(root){
  let queue=[];
  queue.push(root);
  while(queue.length>0){
    let current=queue.shift();
    console.log(current.val);
    if(current.left){queue.push(current.left)}
    if(current.right){queue.push(current.right)}
  }
}

5. 将二叉查找树变为有序的双向链表（待补充）

这个题目实际上不困难，但 LeetCode （Problem 114） 上明确要求需要直接对原 TreeNode 进行调整，而不是新建一个链表，如果不考虑限制，直接进行遍历后构造链表即可，下面是一个实现，就地转换为双向链表待补充。

/**
 * @param {TreeNode} root
 * @return {LinkedList} 
 */
 class LinkedList{
  constructor(val){
    this.val=val;
    this.prev=null;
    this.next=null;
  }
}
function treeToLinkedList(root){
//先写一个简单版本的，就是占用额外空间，生成一个新的列表
  const preorder=[];
  function preOrder(node){
    if(!node){return}
    preorder.push(node.val);
    if(node.left){preOrder(node.left)}
    if(node.right){preOrder(node.right)}
    return preorder;
  }
  let list=preOrder(root);
  console.log(list);
  if (!list){return}
  let currentListItem=new LinkedList(list.shift());
  currentListItem.prev=null;
  while(list.length>0){
    let nextListItem=new LinkedList(list.shift());
    currentListItem.next=nextListItem;
    nextListItem.prev=currentListItem;
    currentListItem=nextListItem;
  }
  return currentListItem;
}

6. 求二叉树第K层的节点个数

递归解法

原理是二叉树的第K层的节点个数等于二叉树左子树第K-1层节点个数加上二叉树右子树第K-1层节点个数。

function NumOfKthLevel(root, k) {
  if (k < 0) {return 0}
  if (root === null) {return 0}
  if (root !== null && k === 1) {return 1}
  return NumOfKthLevel(root.left, k - 1) + NumOfKthLevel(root.right, k - 1)
}

非递归解法

单独列出本解法是因为在实现的过程中，可以在广度优先搜索的同时进行记录，直接实现了打印二叉树每一层的各个节点值，下列方法中若直接返回数组nums就是每一层的节点，对nums各项子数组求长度就是各层的节点个数。

/**
 * @param {TreeNode} root {Number} k
 * @return {Number} 
 */
function numOfKlevel(root,k){
//这道题使用广度优先搜索BFS来解决，暂不考虑root为null
  const queue=[];//用于BFS
  const nums=[];//用于存储各层节点数
  let level=1;//层数
  nums[level-1]=[];
  let currentLevelCount=1;//当前层未打印个数
  let nextLevelCount=0;//下一层结点个数
  queue.push(root);
  while(queue.length>0){
    let current=queue.shift();
    nums[level-1].push(current.val);
    currentLevelCount--;
    if(current.left){
      queue.push(current.left);
      nextLevelCount++
    }
    if(current.right){
      queue.push(current.right);
      nextLevelCount++
    }
    if(currentLevelCount===0){
      if(nextLevelCount===0){break}
      console.log(nextLevelCount);
      currentLevelCount=nextLevelCount;
      nextLevelCount=0;
      level++;
      nums[level-1]=[];
    }
  }
  if(k>nums.length){return 0}
  return nums[k-1].length;
}

7. 求二叉树中叶子节点的个数

/**
 * @param {TreeNode} root
 * @return {Number} 
 */
function numOfLeaf(root){
  if(!root){return 0}
  if(!root.left&&!root.right){return 1}
  return numOfLeaf(root.left)+numOfLeaf(root.right)
}

8. 判断两棵二叉树是否结构相同

/**
 * @param {TreeNode} root1，root2
 * @return {Boolean} 
 */
function compareStruct(root1,root2){
  if (root1===null&&root2===null){return true}
  if((root1!==null&&root2===null)||(root1===null&&root2!==null)){return false}
  return(compareStruct(root1.left,root2.left)&&compareStruct(root1.right,root2.right))
}

9. 判断二叉树是不是平衡二叉树

本题需要使用获取二叉树高度的方法 heightOfTree

function isBalanced(root) {
  if (root === null) {return true}
  if(Math.abs(heightOfTree(root.left)-heightOfTree(root.right)) > 1) {return false}
  return(isBalanced(root.left) && isBalanced(root.right))
}

10.求二叉树的镜像（翻转二叉树）

这是网红题目，源自 Homebrew 的作者 Max Howell 去面试 Google 不会做这个题被拒后在 Twitter的吐槽，然而这道题实际上非常非常的简单，这同时是 LeetCode Problem 226。

function invertTree(root) {
  if (!root) {
    return null
  }
  let right = root.right;
  root.right = root.left;
  root.left = right;
  invertTree(root.left);
  invertTree(root.right);
  return root
}

11. 求二叉树中两个节点的最低公共祖先节点

本题是 LeetCode Problem 236，本人实现的不够简洁，虽然不太清楚为什么 LeetCode 显示内存使用少于 100% JavaScript程序，运行速度也超过39%……

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */

const lowestCommonAncestor = function(root, p, q) {
function searchParent(root,val){//查找某个值的父节点
  if(!root){return null}
  if(root.val===val){return null}
  if((root.left&&root.left.val===val)||(root.right&&root.right.val===val)){return root}
  return searchParent(root.left,val)||searchParent(root.right,val);
}
//检查某个值在二叉树中是否存在
function treeContain(root,val){
  if(!root){return false}
  if(root.val===val){return true}
  return treeContain(root.left,val)||treeContain(root.right,val)
}

// console.log(searchParent(root, 7));
//  console.log(treeContain(root, 210));
//返回某val值在二叉树中节点的层数（该值已经确认在二叉树中)，这个完全参考的第6题
function levelInTree(root,val){
  //这道题我们使用广度优先搜索
  const queue=[];
  let level=1;//存储当前层数
  queue.push(root);//根直接入队列
  let currentLevelCount=1;//存储当前层数中剩余项
  let nextLevelCount=0;//存储下一层数中剩余项
  while(queue.length>0){
    let current=queue.shift();//出栈一个
    if(current.val===val){return level}//检查是不是val值
    currentLevelCount--;
    if(current.left){
      queue.push(current.left);
      nextLevelCount++
    }
    if(current.right){
      queue.push(current.right);
      nextLevelCount++
    }
    if(currentLevelCount===0){//当前层的没了，就得换层了
      currentLevelCount=nextLevelCount;
      nextLevelCount=0;
      level++;
    }
  }
  return -1;//要是没找到，就返回-1，当然别的值也行
}
  if(q===root||p===root){return root}
  let minLevelItem=levelInTree(root,p.val)<=levelInTree(root,q.val)?p:q;
  let maxLevelItem=levelInTree(root,p.val)<=levelInTree(root,q.val)?q:p;
  let currentParent=minLevelItem;
  if (currentParent===root){return root}
  while(!treeContain(currentParent,maxLevelItem.val)){
    currentParent=searchParent(root,currentParent.val)
  }
  return currentParent;
    
};

12. 求二叉树中节点的最大距离（未完成）

待补充。

13.由先序遍历序列和中序遍历序列重建二叉树

实际上这道题目能够扩展为三个题目，还可以由前序和后序构造，由中序和后序构造，LeetCode上均有对应题目：

  • LeetCode 105 前序和中序构建
  • LeetCode 106 中序和后序构建
  • LeetCode 889 先序和后序构建

实现上包括中序遍历的都要简单一些，由先序和后序构建则要复杂一些，这里只列由前序和中序构建的代码：

/**
 * @param {Array} preorder
 * @param {Array} inorder
 * @return {TreeNode}
 */
function constructBinaryTree(preorder, inorder) {
  //先序第一个就是根节点，在根据根节点在中序中的位置，可以得到左子树和右子树，根据长度又能找到左子树的根节点，递归
  if (preorder.length === 0) {
    return null
  }
  let currentRoot = preorder[0];
  let root = new TreeNode(currentRoot);
  let position = inorder.indexOf(currentRoot);
  let leftInOrder = inorder.slice(0, position);
  let rightInOrder = inorder.slice(position + 1);
  let leftPreOrder = preorder.slice(1, leftInOrder.length + 1);
  let rightPreOrder = preorder.slice(leftInOrder.length + 1);
  root.left = constructBinaryTree(leftPreOrder, leftInOrder);
  root.right = constructBinaryTree(rightPreOrder, rightInOrder);
  return root;
}

14. 判断二叉树是不是完全二叉树

//使用广度优先搜索，思路是不管是不是null,都入栈，出栈的时候发现是null，那后面一定都是null或者空队列，否则就不是完全二叉树
/**
 * @param {TreeNode} root
 * @return {Boolean}
 */
function isComplete(root) {
  const queue = [];
  queue.push(root);
  while (queue.length > 0) {
    let current = queue.shift();
    if (current) {
      queue.push(current.left);
      queue.push(current.right);
    } else {
      while (queue.length > 0) {
        if (queue.shift()) {
          return false;
        }
      }
    }
  }
  return true;
}

15. 求某个值在二叉树中节点的层数

本题是第6题的一个延伸，实际上使用的方法完全一样。

/**
 * @param {TreeNode} root
 * @param {Number} val
 * @return {Number}
 */
function levelInTree(root, val) {
  //这道题我们使用广度优先搜索
  const queue = [];
  let level = 1;//存储当前层数
  queue.push(root);//根直接入队列
  let currentLevelCount = 1;//存储当前层数中剩余项
  let nextLevelCount = 0;//存储下一层数中剩余项
  while (queue.length > 0) {
    let current = queue.shift();//出栈一个
    if (current.val === val) {
      return level
    }//检查是不是val值
    currentLevelCount--;
    if (current.left) {
      queue.push(current.left);
      nextLevelCount++
    }
    if (current.right) {
      queue.push(current.right);
      nextLevelCount++
    }
    if (currentLevelCount === 0) {//当前层的没了，就得换层了
      currentLevelCount = nextLevelCount;
      nextLevelCount = 0;
      level++;
    }
  }
  return -1;//要是没找到，就返回-1，当然别的值也行
}

二叉数的可视化表示

留个坑待填

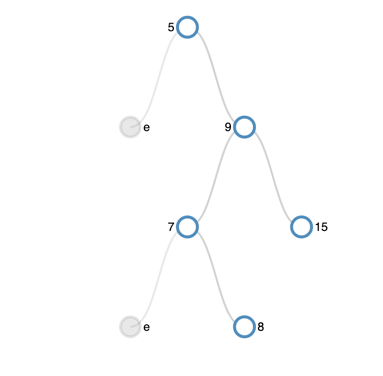
LeetCode Problem 655 是要求我们图形化二叉树，不过我想要的是更美观一点的那种，不是简单的打印出来并用*号填充没有值的部分。本来想自己实现一个，打算用原生 CSS+JS 试一下，给每行定义了48个圆形，根据二叉树高度判断行数，根据行数来确定各行显示哪些节点，然后进行值填充，最后把是null值的节点也隐藏掉，两行节点之间增加一行用于加连线，通过transform 属性给矩形画对角线完成。但是实践中才发现各层节点之间的距离差异太大，想把这个连线画上去实在太难，只能放弃。

binary-tree-visualize-fail.png

这是计划的效果，如果行数少的话会美观一点，这个坑以后再填。

网络资源

万能的互联网搜索一下，还是有一些资源的，但并没有让我满意的，我的初衷是实现一个美观一点的可视化二叉树的方法，主要用于截图展示，因为现在网上的太多二叉树的图，实在太难看了。下面的资源并不能将你的数组方便的变成二叉树用于展示，待找到好的资源再来补充，当然最好是自己能写一个。

通过 D3.js 实现的二叉搜索树

d3-binary-search-tree.png 点击访问 CodePen 地址

然而我觉得挺难看的，不过确实没搜索到好看的。

算法神站 Visualgo的

点击访问

另一个比较美观的

点击访问

后记

基本上把二叉树常用的方法实现了一下，后续有精力再写一下二叉搜索树和 AVL 树，等我搞明白了红黑树那天说不定也会顺便补充一下。

在 Twitter 上讨论 • 在 GitHub 上查看